重積分の定義について
重積分の定義について,1変数の場合から書きました。(リーマン)積分のちゃんとした定義をはじめて書き下しました。ちゃんとしてないかもしれません。




こうやって長方形の足し算で定義されたリーマン積分が,微分と関係しているっていう微積分学の基本定理,すごいですよね。それについてもちゃんと書き下しておきたいと思っています:)
次
未定
前
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
ガウスの法則
ガウスの法則について書きました。分かったようで分からないようで分からないです。重力と違って日常の間隔がないので,直感的にというのはなかなか厳しい感じがしますよね。




ちなみ最後の方の一般的な閉曲面について逃げていますが,べつにこの場合でもちゃんと計算できるようです。対象な球面だけで勘弁して下しあ。
電磁気学はむずかしいですね。
次
未定
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
ベクトル場・スカラー場・流束について
ベクトル場と流束とスカラー馬について書きました。タイポですが残しておきます。ベクトル場とか流束とかわかるようでわからんようでわかるような概念ですが,これは電磁気学で超便利なものなのでぜひとも習熟したいところです。でなければ四元数でがんばることになってしまいます。




しかし,よくこういう抽象的な概念を定式化しますよね。式考えてる中で,本当にこれでいいのか?って,無限に悩みそうな気がします。
次
未定
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
ベクトルの微分
ベクトルのビブンについて書きました。直交座標系で考えるならばとくに何も気にせずにビブンビブンしとけばいいと思います。単位ベクトルが時間変化するような座標系では要注意です。


ベクトルの動きを追えば,なんで円運動の加速度が中心方向を向くのかが理解できますね。
次
未定
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
角運動量保存則はどうやって導くのか
角運動量保存則がどうやって導かれるのかについて書きました。運動量保存則とほとんどやっていることは同じです。外積の微分に少し注意する必要があります。



古典力学はけっこうなあなあで,適当に書いてしまっているのでいつの日かちゃんと書き直したいですね。
次
未定
前
角運動量
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
群の定義について
群の定義について書きました。はじめて見たときはなんと抽象的な概念でしょう,と思ったのちにすぐ忘れたんですが,今回は複素数を学び直す中で演算を表す記号のもっと一般的なものはなんかないんかと疑問を持った中で調べたのですんなり入り込むことができました。



やはり主体的に望むことは大事だということでしょうか。あとは興味を持ったものから取り組むってところですかね。数学自体が抽象化に興味があるのだとしたら,数学への取り組み方の抽象化にも興味を持ちたいところですよねなどと思っているところです。
次
未定
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
スカラー三重積とベクトル三重積
スカラー三重積とベクトル三重積について書きました。こいつらは名前で脅しに来ているだけだと思いました。なんとなくですが,これらのもっと一般化した構造が知りたいと思ったりしました。特に外積のもっと広い概念,ウェッジ積でしたか?そいううところ,おもしろそうですよね。



次
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
ベクトルの基礎
ベクトルの基礎について色々書いています。中身ほとんどないです。というか投稿する段階になって位置ベクトルの欄がひどいことになっているのに気づいてしまいました。このままにしておきましょう。




次
未定
前
なし
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
複素数の定義について
複素数の定義について,3つの角度から書けていません。多項式の剰余としての定義については環について学ばなければいけなさそうです。ふはは。
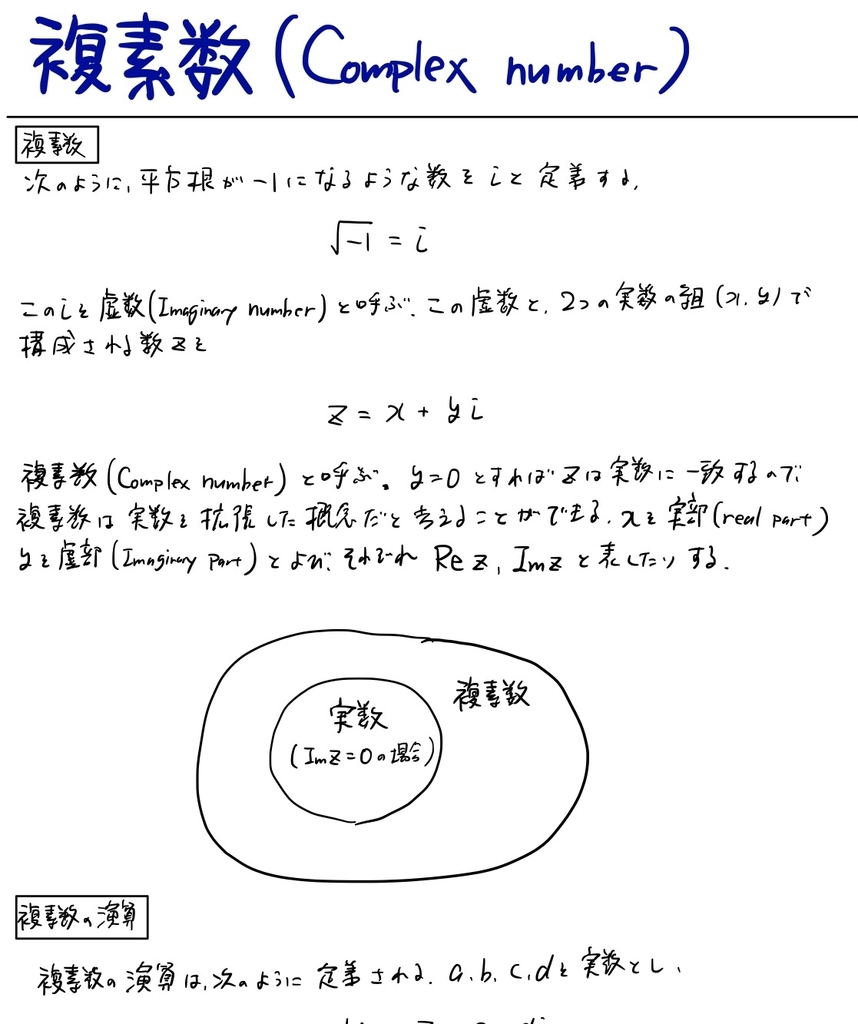



複素数を定義する段階で,そういえば高校の頃にこの実部と虚部の間にある+の記号はどういう意味の+なんだろうと思ったことを思い出しました。そこで気になって色々調べたら,抽象代数学あたりから見てみるとスッキリするらしいと知ったので,代数学にもちろっと手を出してみようと思ったのでした。
実際のところまだまだ疑問がありまするが,ゆっくり見ていくことにします。というかこのページ自体がまだ全然書きかけでした。
次
未定
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
和空間と直和空間
運動量保存則について
運動量保存則がどこから導き出されるのかについて書きました。単刀直入に言えばニュートンの第3法則,すなわち作用反作用の法則を仮定すると自然に出てきます。そんで,運動量保存則は実験とかで確かめられるので,逆の視点からんじゃ,ニュートンの第3法則も間違ってなさそうやんって言うことができますね。



運動量についての記事を書く前に保存させちゃいました。
前
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
www.takagrow.com
ニュートンの運動の三法則
ニュートンの運動の三法則について書いています。ニュートンの法則は,慣性系という考え方に慣れるとまったく違った見え方になるんですね。おもひろいです。(おもしろいと世界は広いなあ,の合わせ造語)



物体を観察している時に,自分の状況にも気をつけなければいけない。もっというと相手が運動しているように見えるのは自分が動いてるだけなのかもしれない。っていう相対的な考え方に至るには,かなり高度な認知能力が必要だよなあと思いました。ガリレオさんやデカルトさん,ニュートンさんはすごいんですねえ。
前
次
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
www.takagrow.com
熱容量・比熱・モル比熱について
熱力学における熱容量・比熱・モル比熱という考え方について書いています。このようにして,一般的な熱容量という考え方を述べてから,経路に分けて名前をつけていく方が好きです。


僕がパラパラ眺めた教科書や資料では,熱容量を初めから経路で分けたまま紹介していくという形式が多いように感じました。より一段高い視点から決めたほうがスッキリ見えると思います。断熱熱容量というものは通常あまり考えることはないですが,定義としては考えることができます。
比熱やモル比熱は,物体をg単位,mol単位でまとめて扱うことによって熱容量を現実的に使いやすいようにと考えられたものですね。ちなみに温度についてまだこのプログでは定義できていないので,ズルをしていることになるのですが,おいおいしっかり書こうと思うのでご容赦ください。(ペコリ)
前
www.takagrow.com
次
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
www.takagrow.com
熱力学第一法則について
熱力学第一法則について書きました。この第一法則の解釈の一つとして,第1種永久機関(自身のエネルギーを減少させることなく外部に仕事をする機関)を作ることができないというのがありますね。


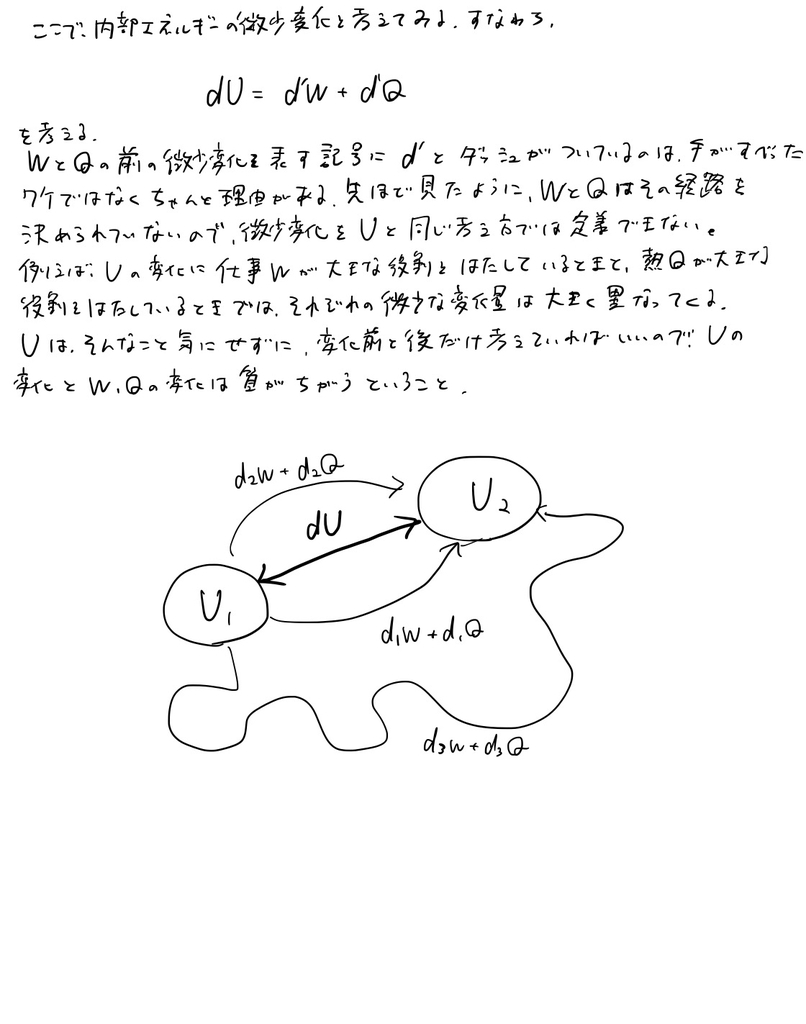
熱力学の第一法則にはいろいろな表現の仕方があって,仕事の定義において正負のおきかたが違ったり,熱量が左辺に来ていたり,微小変化の形で書いてあったりしますが,それらは表現の仕方が異なるだけで同じことを言っています。
ある系の内部エネルギーに着目した時,その変化は必ず仕事と熱の和で表すことができて,それで取りこぼしたものはないよということです。なので実際,一つ前のページでもすでにこの話題を取り扱っていたわけです。
高校では内部エネルギーを考えるためにいきなり理想気体(分子の質量も,位置エネルギーも考慮しない)を考えたわけですが,この段階ではまだ,理想気体を考えてモデル化してしまう前にもっと広い視点を持って眺めています。高校の時に何も分かってなかったのが分かってきておもしろいです。
前
www.takagrow.com
次
www.takagrow.com
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長
内部エネルギー
熱力学における内部エネルギーについて書きました。自分自身の熱力学に対する理解がかなり浅いので,書くためにいろいろな本や資料を読んでいるときにすべてが新鮮に感じられてとても楽しめました。



ただ,理解が浅いのでこれはあくまで下書きという感じです。これをきっかけに熱力学をジワジワ攻略していきたいと思います。さしあたっての目標はエントロピーあたりをしっかりと自分の言葉で書き下すことです。よろしくおねがいします。
間違いがあればご指摘いただけると幸いです。
全ての学習記録はコチラです。
サイトマップ - たかくんの成長



